Gradient Descent

← Previous Lesson | Home

Gradient Descent is an iterative optimization algorithm used to adjust a model’s parameters in order to minimize its cost function. It’s a fundamental cornerstone of machine learning, and enables the “learning” part. It’s used in Neural Networks and Deep Learning models as well.

Our linear regression cost model $J(w,b)$ only has 2 params, but we can use Gradient Descent on many various cost functions that have more than 2 parameters.

The cost function plotted below is NOT the squared error cost function for linear regression, thus there are multiple local minima (multiple minimum error rates)

When initiating Gradient Descent, you choose a random point to start. For example, during linear regression we usually start at the coordinates $(0,0)$ or $w=0,b=0$ . For the below example let’s start at the top of the crest where our happy little person is. Your goal is to find your way to one of the troughs, or local minima, as efficiently as possible.

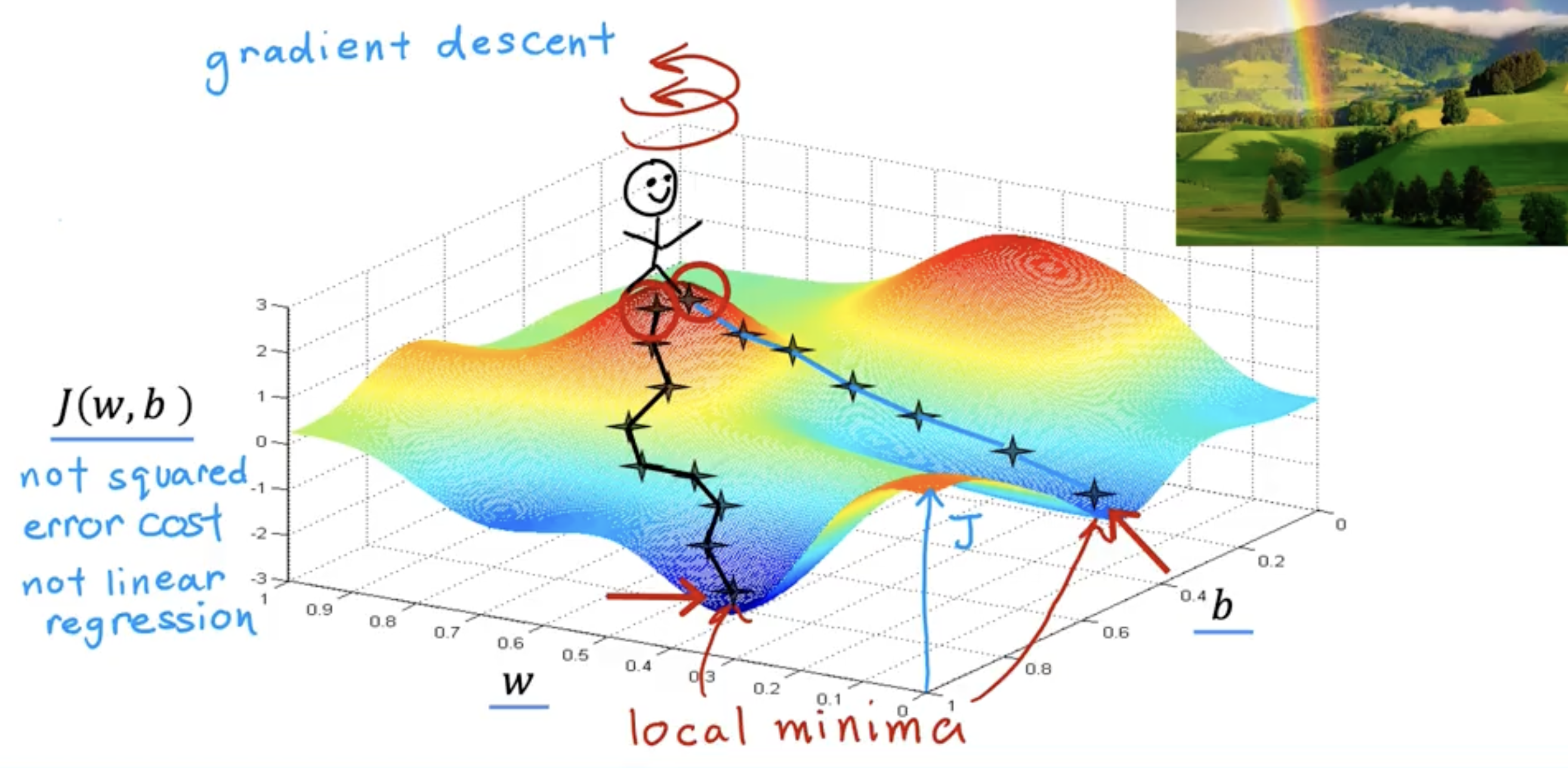
The Gradient descent algorithm essentially does a 360 turn at your current point and asks “if I were to take a tiny little baby step in one direction, and I want to go downhill as quickly as possible to one of these valleys. What direction do I choose to take that baby step?” That direction has the “steepest descent.”

We essentially repeat this process iteratively until we can no longer find a “steepest descent,” thus leaving us at our local minima/minimized error rate.

NOTE: you can see there are 2 paths that could lead you to two different local minima depending on where you start. Even though the origin point of the two paths are right next to each other, they arrive at different local minima.

---

So what is the Gradient Descent Algorithm?

$w=w-\alpha \frac{\partial J(w,b)}{\partial w}$

• $\alpha$ = The learning rate
• $\frac{\partial J(w,b)}{\partial w}$ = The derivative (technically a partial derivative since we are only changing so many dimensions at a time while freezing the rest. I will explain more later)

When calculating the gradient for multiple params, we need to update all the params simultaneously. This is because we do NOT want to update params during 1 pass.

If we update w while calculating b, we would get the wrong next param value.

Gradient descent is an algorithm $w=w-\alpha \frac{\partial J(w,b)}{\partial w}$ for finding values of parameters w and b that minimize the cost function J. What does this update statement do? (Assume $\alpha$ is small.)

Answer: Updates the parameter $w$ by a small amount, in order to reduce the cost $J$.