Linear Regression Model
Most widely used learning algorithm in the world today. It just means fitting a straight line to your data. An example real-world problem is house sizes and prices.
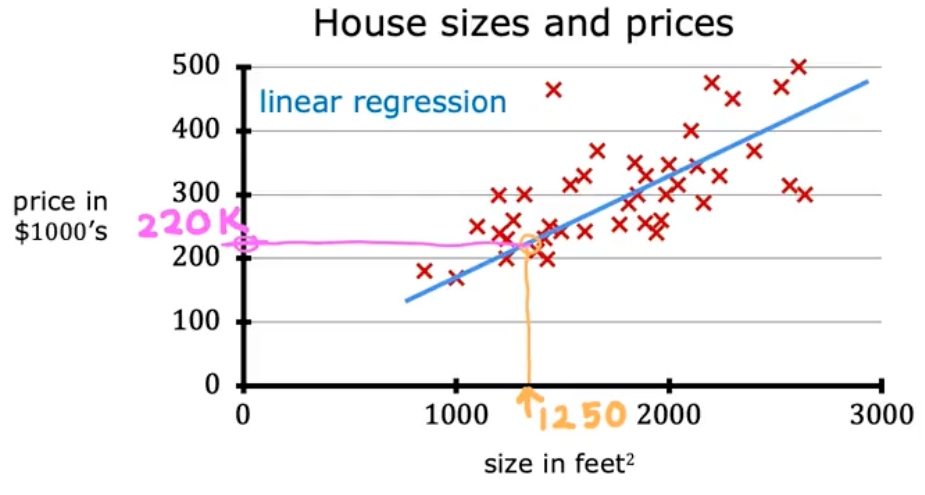
Linear Regression Models are just one type of a Supervised Learning Model.
Regression models predict numbers. ANY supervised learning model that predicts a number is a Regression Problem.
In contrast with Regression models, the other most common type of Supervised Learning Model is Classification models.
- In Classification, there are a small number (finite) number of outputs
- In Regression, there are an infinite number (continuous) number of outputs
ML Terminology/Notation

- Training Set: Data used to train the model
- x: “input” variable. Also known as “feature”
- y: “output” variable. Also known as “target”
- m: Total number of training examples
- (x, y): Single training example
- x1: The first training examples input
- y1: The first training examples output
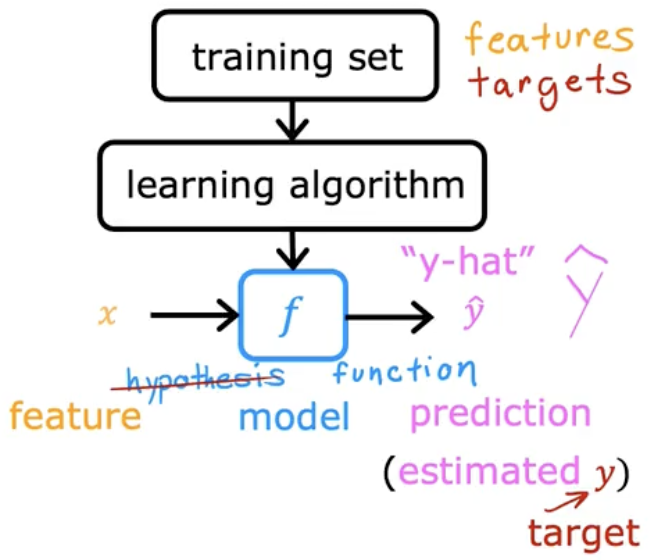
A training set includes
- input features
- output targets
They are both required and fed to the Learning Algorithm. Your supervised learning Algorithm will then produce a function (f). (historically called a ‘hypothesis’). This function is really called the Model.
Then, you can feed a new input feature to the function, and the function will then produce a new output called y-hat (ŷ). If you refer to a models output as just y without the hat, then this refers to the target, which is the actual true value in the training set. in contrast ŷ is an estimate.
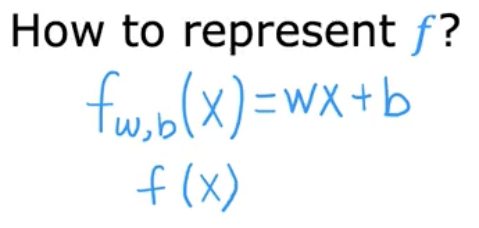
When designing a learning algorithm, the key question is: “What is the math formula used to compute f?”
For now, let’s keep our function as a straight line. So this would look like:
fw, b (x) = wx + b
The values chosen for w and b will determine ŷ based on input feature x. Sometimes we will refer to this same notation as f(x) as shorthand
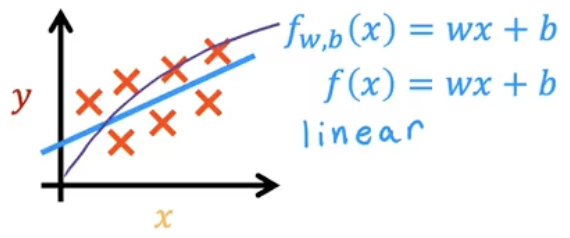
When plotting our data the feature (x) is on the horizontal axis and the target (y) is on the vertical.
The algorithm learns from our data and generates the best-fit line, which is our function:
fw, b (x) = wx + b
or more simply
f(x) = wx+b
This function is making predictions for y using a streamline function of x.
You may ask, why use a linear function (fancy word for straight line) as opposed to a curve or parabola?
We are just using linear functions for now until we can build up to more complex non-linear functions.
We are using Linear Regression models with 1 variable. This means we have a single feature.
Another name for a linear model with one variable is Univariate Linear Regression
If currently we are just using the size of a house as our feature to predict the cost, we may in the future want to use the size of the house in addition to other variables like the number of rooms.
Which of the following is the output or "target" variable? → ŷ, y, m, x?
Answer: y